Main

LP 791-18d was detected through 127 h of dedicated, near-continuous Spitzer observations of LP 791-18, one of the smallest stars known to host planets. LP 791-18 was previously known to host the hot super-Earth LP 791-18b on a 0.94-day orbit and the sub-Neptune LP 791-18c on a 4.99-day orbit, both discovered in June 2019 by the Transiting Exoplanet Survey Satellite (TESS)4, but both without radial-velocity confirmation or mass measurements.

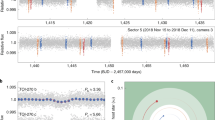
Two transits of the newly discovered LP 791-18d are clearly visible in the 127-hour-long Spitzer light curve (Fig. 1), in addition to transits of the previously known planets LP 791-18b and c. We subsequently confirmed LP 791-18d’s ephemeris using ground-based telescopes and discovered that the new LP 791-18d opens the system to mass measurements through transit timing variations (TTVs). We therefore complemented our observations of this system with a large multi-year, multi-telescope transit campaign totalling 72 transit observations between 2019 and 2021 including 43 transits of the Earth-sized planet LP 791-18d and 29 transits of sub-Neptune LP 791-18c (Methods, Extended Data Tables 1 and 2 and Extended Data Fig. 1). Our detection of TTVs, further discussed below, confirms the planetary nature of the LP 791-18 transit events by evincing the mutual gravitational interaction between planets c and d.

Fig. 1: TESS and Spitzer light curves of LP 791-18.
figure 1

a, TESS observations of LP 791-18 taken between 1 and 25 March 2019 detrended using a Gaussian process with a fixed length scale of 1.0 days, with the transit times of planets b, c and d indicated. Only the transits of planet c are visible by eye. b,c, PLD-corrected and detrended Spitzer observations deliberately scheduled to capture two transits of planet c, with the first transit appearing much deeper due to overlap with the transit of planet b (b). The signatures of all three planets are visible by eye in the processed Spitzer data, and are also shown phase-folded in c. d, Snapshot of the orbits of the three planets.

Full size image

The radius of the newly discovered LP 791-18d is consistent with that of the Earth (1.03 ± 0.04 R⊕) and its equilibrium temperature is 395 K for an Earth-like Bond albedo and 305 K for a Venus-like Bond albedo, assuming efficient heat redistribution around the planet. The orbital period of planet d is 2.753 days. In the analysis, we used a revised stellar luminosity (0.00230 ± 0.00001 L⊙) and stellar radius (0.182 ± 0.007 R⊙) based on a newly obtained Infrared Telescopy Facility (IRTF)–SpeX Prism spectrum and publicly available broadband measurements (Methods and Extended Data Table 3). We similarly refined the radius estimate of the sub-Neptune LP 791-18c to 2.44 ± 0.10 R⊕ (Extended Data Table 4). Finally, we derived mass estimates by fitting the 72 mid-transit times of planets c and d using TTVFast transit timing modelling7 in combination with emcee8 (Methods).

TTVs with an amplitude of 4.53 ± 0.43 min are detected for LP 791-18d consistently in the Spitzer and ground-based observations (Fig. 2 and Extended Data Fig. 2). The TTVs constrain the mass of the sub-Neptune LP 791-18c to 7.1 ± 0.7 M⊕ and the mass of the exo-Earth LP 791-18d to \({0.9}_{-0.4}^{+0.5}{M}_{\oplus }\) (Methods and Extended Data Table 4). Comparing the inferred radii and masses to planet interior models, we find that the mass of planet c is significantly below the 25 M⊕ that a purely rocky planet with the measured radius of planet c would have, indicating that planet c retained a significant amount of H2/He envelope and/or a volatile-rich mantle. In interior model grids9,10, a best match to the mass and radius is obtained for scenarios with \({2.0}_{-0.5}^{+0.6} \% \) of the planet’s mass in a H2/He envelope or, alternatively, roughly 50% of the entire planet composed of icy material (Extended Data Fig. 5). Either way, planet c must have been able to hold onto a substantial amount of volatiles or gas. The newly found planet LP 791-18d, on the other hand, is consistent with a rocky, potentially Earth-like, composition given its radius of 1.03 ± 0.04 R⊕ and its mass of \({0.9}_{-0.4}^{+0.5}{M}_{\oplus }\). LP 791-18d is unlikely to harbour any hydrogen atmosphere today, as the maximum amount of hydrogen consistent with the observed planet radius would be unstable to atmospheric escape (Methods).

Fig. 2: TTVs of LP 791-18d.
figure 2

Coloured data points indicate the transit timing measurements obtained with Spitzer (red), LCOGT (green), MuSCAT/MuSCAT2 (dark blue), MEarth (yellow), TRAPPIST (purple), EDEN (brown), ExTrA (pink) and SPECULOOS (grey), compared to the best-fitting TTVFast model (blue curve). The vertical axis represents the deviation from the best-fitting linear ephemeris and the horizontal axis the barycentric Julian date (BJD) of the observation. Dark and light shaded regions illustrate the posterior population of models in the MCMC fit corresponding to 68% and 95% confidence, respectively. TTVs with 4.53 ± 0.43 min chopping amplitude are consistently detected in both the Spitzer and ground-based data, at a phase consistent with the planetary conjunctions of planets c and d. Some transits near BJD of 2458900 were observed with up to four telescopes simultaneously, with points slightly offset horizontally for clarity. Only part of the data set is shown here for clarity, and the full data set of 72 transit timing measurements of LP 791-18c and d is depicted in Extended Data Fig. 2.

Full size image

Together in the same system, the two planets span the small-planet radius valley and offer a rare opportunity to test planet formation and gas envelope evolution models in the previously poorly explored regime of late-M dwarfs. Well-established for FGK-type stars11, recent planet demographics studies of early-to-mid M stars have suggested a similar dearth of planets12, with some suggesting that gas-poor planet formation13, rather than photoevaporation14 or core-powered mass loss15, may dominate the evolution of planets around low-mass stars12. LP 791-18 being the only known late-M-dwarf system with planets spanning the radius valley, we begin to put this hypothesis to the test for late-M dwarfs. We find longer mass-loss timescales for the sub-Neptune LP 791-18c, when compared to LP 791-18d, consistent with the predictions from photoevaporation16 and core-powered mass loss15,17 (Methods and Extended Data Fig. 6). We conclude that both thermally driven mass loss as well as gas-poor formation remain viable formation scenarios for LP 791-18d.

Depending on its formation history, LP 791-18d can therefore host a wide range of plausible atmospheres and amounts of volatiles at its surface. If the core of LP 791-18d had already formed before disc dissipation, LP 791-18d could have captured an early hydrogen-rich atmosphere shortly after formation, similar to the sub-Neptune LP 791-18c orbiting just exterior to LP 791-18d’s orbit. Whereas it was probably short-lived on LP 791-18d (Methods), this hydrogen-rich atmosphere could have triggered magma mantle–atmospheric interactions, possible resulting in the formation of many Earth-oceans worth of H2O by means of H2 oxidization by Fe2+O in the mantle18. A large fraction of this H2O could have safely been harboured in the planet’s interior during the magma ocean phase and would then have outgassed only gradually over geological timescales. In this gas-rich formation scenario, the result could be a highly oxygen-rich, low carbon-to-oxygen ratio, endogenous water world with the total amount of water in the envelope and mantle depending on the intitial FeO content of the magma and the mass of hydrogen accreted during its early formation history18. Alternatively, if LP 791-18d formed as a gas-poor terrestrial planet without primordial gas envelope (gas-poor formation), then the planet could have formed a secondary atmosphere similar to Earth and Venus through outgassing or the accretion of volatile-rich solids. The composition of an outgassed atmosphere would then depend on the complex volatile exchange with the molten interior, governed by redox reactions and volatile solubilities during the magma ocean phase19, and affected by the rate and tectonic setting of volcanism after the magma ocean phase.

The hypothesis of active ongoing outgassing on LP 791-18d is further strengthened by the inferred non-zero forced eccentricity of 0.0015 ± 0.00014 (11σ) resulting from the continued gravitational interaction with the eight times more massive LP 791-18c in near-resonance (Methods and Extended Data Figs. 3 and 4). This non-zero eccentricity introduces significant tidal heating of LP 791-18d’s interior, with the resulting surface heat flux (0.2–0.9 W m−2) up to an order of magnitude larger than the heat flux that Earth’s surface experiences due to the radiogenic and primordial heat in Earth’s interior (Fig. 3 and Methods). For a rocky surface composition, this would result in surface eruptions and volcanic activity, potentially similar to Jupiter’s tidally heated moon Io5,6, which in turn would continuously replenish the atmosphere of LP 791-18d with outgassed, potentially detectable, molecular species. In all modelled scenarios, we consider LP 791-18d in a tidally locked state (Methods) and we find mantle equilibrium temperatures above the solidus temperature of rock, indicating that the mantle of LP 791-18d can maintain a permanent molten silicate layer.

Fig. 3: Internal energy balance of LP 791-18d in the presence of tidal heating.
figure 3

Coloured curves trace the tidal heating per unit surface area \({F}_{{\rm{t}}{\rm{i}}{\rm{d}}{\rm{a}}{\rm{l}}}={\dot{E}}_{{\rm{t}}{\rm{i}}{\rm{d}}{\rm{a}}{\rm{l}}}/4\pi {R}^{2}\) (solid) and the convective heat transport towards the surface Fconv (dashed) as a function of the mantle temperature for the inferred forced eccentricity of LP 791-18d (e = 0.0015). The equilibrium mantle temperature is reached where Ftidal = Fconv (coloured circles). Four sets of curves and equilibrium points are shown across the full range of melt fraction coefficients, with B = 10 shown in yellow, B = 20 in light orange, B = 30 in dark orange and B = 40 in red(Methods). In all cases, as the planet cooled down, equilibrium was reached beyond the solidus temperature (vertical black line), indicating that LP 791-18d has a partially molten mantle due to tidal heating. The surface flux due to tidal heating is 0.2–0.9 W m−2 and, therefore, up to an order of magnitude stronger than Earth’s surface heat flux of 0.0916 W m−2 due to radioactive decay and primordial heat24, probably dominating the internal heat flux budget of LP 791-18d. Strong volcanism, surface eruptions and atmospheric replenishment exceeding those of Earth would be the likely result. For another comparison, the range of inferred heat flux estimates for Jupiter’s moon Io, the most geologically active body in the Solar System, is shown in blue, with the horizontal blue dotted lines indicating the lowest and highest estimates in the literature25.

Full size image

The tidally locked state of LP 791-18d also results in atmospheric dynamics and a climate pattern distinctively different from those of Venus and Earth, with the permanent day side receiving all the stellar insolation. Depending on the planet’s yet-unknown evolutionary history, LP 791-18d may either have entered a Venus-like runaway greenhouse state20,21 and possibly lost all its volatiles to space, or alternatively, LP 791-18d could have entered a ‘collapsed’ regime, in which water began to be captured in permanent cold traps on the night side or at the poles, thereby possibly avoiding the runaway and moist greenhouse regimes altogether22,23 (Methods). Looking forwards, LP 791-18d, being a probably volcanically highly active Earth-sized planet near the inner edge of the habitable zone of a late-M dwarf in a system with a sub-Neptune offers several unprecedented opportunities to advance our understanding of the evolution of Earth-sized planets, the outgassing and atmospheric retention of temperate rocky planets in general, as well as the origin of the radius valley (Fig. 4 and Methods).

Fig. 4: Temperature and radius of small transiting planets with measured masses amenable to transit spectroscopy.
figure 4

Colours indicate the expected strength of spectral features introduced by a CO2-dominated atmosphere (five scale heights; right labels on colour bar), whereas point sizes indicate the relative SNR achievable per transit in the photon-noise limit, akin to the Transit Spectroscopy Metric26. For rocky planets, both quantities (colour and marker size) are essential in determining whether a planet is a good target for atmospheric characterization due to the separate limits introduced by photon noise and a potential systematic noise floor27,28,29. All planets with expected atmospheric signals greater than 7 ppm for CO2 atmospheres are labelled by name, albeit many of them would require transit depth precision of only a few ppm for significant molecular detections (purple labels). Small planets orbiting LP 791-18 and TRAPPIST-1 (yellow, orange) are unique in terms of the strength of their atmospheric signatures as well as their number of transit events per year. LP 791-18 and TRAPPIST-1 also offer the advantage that they can be observed with the JWST–Near Infared Spectrograph prism without saturation to simultaneously obtain 0.6–5.3 μm. The diffuse vertical stripes near 1.4–1.7 R⊕ (light blue) and 1.7–2.0 R⊕ (grey) highlight the locations of the radius valleys for M stars12 and FGK stars11, respectively. Note that planets that host H2/He-rich atmospheres can show substantially stronger spectral features due to their larger scale heights (left labels on colour bar). Such atmospheres are believed to be more common for planets with radii beyond the radius valley11,30. Equilibrium temperatures are shown for a Bond albedo of AB = 0.3 similar to Earth.

Full size image

Methods

Stellar characterization

We refine the stellar radius of LP 791-18 reported in the TESS Input Catalog v.8 (refs. 4,31) using the same method as used for TRAPPIST-1 and other late-M dwarfs32. For that, we construct an expanded 0.3–17 μm spectral energy distribution (SED) by combining a newly obtained IRTF–SpeX Prism spectrum of LP 791-18 at 0.7–2.52 μm taken on 23 December 2020 with publicly available SDSS, PS1, 2MASS and WISE broadband measurements (Extended Data Table 3). Absolute calibration of IRTF–SpeX Prism spectrum is performed using the overlapping photometric measurements, allowing for an offset and linear trend across the spectrum. We then fill any remaining gaps in wavelength space between 0.3 and 17 μm with linear interpolation in logarithm space, and we complete the SED with a Rayleigh-Jeans tail below 0.3 μm and a Wien tail beyond 17 μm, both using the effective stellar temperature inferred from spectroscopy4 (2,960 K). Once the SED is built, we then infer the total bolometric luminosity by scaling the SED using the measured Gaia eDR3 parallax distance of 26.65 ± 0.03 pc and integrating it over all wavelengths. We find a stellar radius of 0.182 ± 0.007 R⊙ for LP 791-18. Our stellar radius estimate is consistent with that of ref. 4. for LP 791-18 (0.171 ± 0.018 R⊙) albeit with smaller radius uncertainty and inferred on the basis of the empirical reconstruction of the full SED of LP 791-18. Our inferred radius is also consistent with the overall trend in interferometric radii measurements of main-sequence late-M stars33, in which measurements tend to indicate slightly inflated radii versus solar-metallicity models.

Transit observations

In this work, we observed a total of 72 transits of the newly discovered exo-Earth LP 791-18d and the sub-Neptune LP 791-18c using the Spitzer Space Telescope and many ground-based astronomical facilities including the Las Cumbres Observatory Global Telescope (LCOGT) network34, MEarth35, TRAPPIST-N/S36, ExTrA37, MuSCAT38, MuSCAT2 (ref. 39). SPECULOOS40 and the VATT and Kuiper telescopes of the EDEN network41 . Our Spitzer observations were initially undertaken to investigate the possibility of additional terrestrial planets in the system because such planets could be dynamically stable, but could have been missed by TESS. Owing to the faintness of LP 791-18 at visible wavelengths, the TESS light curve lacked the necessary photometric precision to detect planets with radii smaller than roughly 1.2 R⊕ at periods longer than about 1.5 days. Spitzer observed at 4.5 μm nearly continuously for 5 days from 14 to 19 October 2019, except for a 5-h break for data downlink starting 17 October at 23:30. The observations were timed to also capture two transits of planet c, with at least 2 h of baseline observations before the first transit and following the second transit. In addition to the previously known planets, the observations revealed two transits of LP 791-18d. Motivated by the detection of TTVs, we then complemented our Spitzer observations of this system with a large multi-year, multi-telescope transit campaign, consisting of 43 transit observations of the Earth-sized planet LP 791-18d and 29 transits of sub-Neptune LP 791-18c (Extended Data Tables 1 and 2 and Extended Data Fig. 1).

Initial Spitzer light-curve analysis

Our near-continuous 127-hour Spitzer light curve is divided into six light-curve segments, which we initially extract and inspect as separate light curves. For that, we first extract the photometry for each segment using a set of fixed circular apertures with sizes ranging from 1.5 to 5 pixels. For each exposure, we estimate and subtract the sky background, calculate the centroid position of the star on the detector array and then calculate the total flux within the aperture radius42. We find an aperture radius of 3 pixels to produce the lowest photometric scatter for all six segments. Following standard procedure, we detrend our Spitzer light-curve segments against a drift in time and intrapixel sensitivity variations using the pixel level decorrelation (PLD) approach42,43. Our systematics model is given by the following equation:

$$S({t}_{i})=\frac{\mathop{\sum }\limits_{k=1}^{9}{w}_{k}{D}_{k}({t}_{i})}{\mathop{\sum }\limits_{k=1}^{9}{D}_{k}({t}_{i})}+m{t}_{i},$$
(1)

where Dk(ti) represents the raw flux in each of the nine central pixels in the target’s point spread function at time ti of the ith exposure in the photometric time series42. The nine PLD coefficients wk and the linear slope m for the sensitivity drift with time are systematic parameters that are simultaneously sampled with the transit model parameters as described below.

We first perform an initial inspection of the Spitzer data by detrending each light-curve segment separately. We carefully inspect the resulting detrended photometry for decreases resembling transit-like events. In additional to the predicted transits of LP 791-18b and c, we identify two new transit events at the barycentric Julian dates (BJD) = 2458772.16 and BJD = 2458774.9 caused by planet d. We double check that these events do not align with any shift in the background flux or shift in the position of the star’s centroid. The transits of planet d are marked in purple in Fig. 1 and we discuss the sensitivity of the light curve to transiting planets more quantitatively below.

Joint light-curve fitting

To determine the properties and orbits of each planet in the LP 791-18 system, we jointly analyse the TESS, Spitzer and ground-based transit photometry using ExoTEP, a modular tool designed to jointly analyse many transits from different instruments with diverse systematics models30,42,44. The analysis makes use of the AI-MCMC Ensemble sampler emcee package8, combined with the batman package for efficient transit light-curve modelling45. We jointly fit all observed transits of each planet and derive the joint posterior distribution of the transit light-curve model parameters, the systematics model parameters for the Spitzer and ground-based light curves, and a photometric scatter value for each transit light curve. The transit light-curve model for a given planet shares the same impact parameter b and semimajor axis a/R*, with only the transit depth and the limb darkening coefficients assigned separately for each instrument bandpass.

For Spitzer, we simultaneously fit the PLD systematics model parameters described above, whereas the TESS and ground-based transits are detrended before fitting. For the TESS observations, we use the TESS Presearch Data Conditioning Simple Aperture Photometry46,47,48 as produced by the TESS Science Processing Operations Center49, which have been further detrended using quaternions to remove non-astrophysical systematics. To remove any remaining systematics, the TESS light curve was detrended with a Gaussian process with squared exponential kernel and a fixed length scale of 1.0 days. The LCOGT light curves are extracted using the open-source tool AstroImageJ50, and like all ground-based light curves, are detrended against airmass. The MEarth transits, which initially showed systematics possibly caused by water column variation, were additionally detrended using a spline fit that excluded the in-transit data. The first transits of planet b and c in the Spitzer data are overlapping and, for this case, we fit the transits of planet b, planet c and the PLD systematics model simultaneously.

For limb darkening, we use the priors on the quadratic limb darkening coefficients determined for the TESS light curves of LP 791-18 (ref. 4). For the ground-based instruments we use equivalent priors determined with LDTK51 as listed in Extended Data Table 3. For Spitzer, we choose to first fit the deep high-signal-to-noise ratio (SNR) Spitzer transits of planet c to empirically determine the 4.5 μm quadratic limb darkening coefficients for the star LP 791-18. The resulting Spitzer coefficients are then used as priors when fitting planets b and d. The photometric scatter is a free parameter for each transit, except for the TESS data, for which only one scatter parameter is shared by all transits as the overall TESS light curve has a near-constant scatter dominated across photon noise.

The Markov chain Monte Carlo (MCMC) fit for each planet is performed with four walkers per fitting parameter and run for a total of 16,000 steps, much longer than needed for formal convergence. Disregarding the initial 60% of our chains as burn-in, the resulting transit parameters and calculated properties are recorded for each planet in Extended Data Table 4. Transits from ExTrA and SPECULOOS (SSO I+z band) are not included in the joint fits, but were used in the TTV analysis. The ExTrA observations were detrended and fit using the package juliet52 with Gaussian detrending, and with all transit parameters but the timing fixed to the results of our joint fit. The SPECULOOS and/or SSO (I+z) observations are detrended using polynomials of variable order in airmass, background and position53.

TTV analysis

To determine the masses and orbital parameters of planets c and d, we first infer the mid-transit time for each observed transit of planet c and d by fitting each transit observation individually with ExoTEP30,42,44. We include Gaussian priors on all transit parameters other than the mid-transit time on the basis of the best-fit estimate from the joint fit. For Spitzer, we do a high-cadence fit directly on the basis of the tens of thousands of 2-s long exposures. All resulting light-curve fits are shown in Extended Data Fig. 1, with all the transits lined up to the mid-transit times from the best-fitting TTV model.

On the basis of the inferred mid-transit-timing estimates, we then determine the joint posterior distribution of the masses and orbital parameters of planets c and d by modelling and fitting the mid-transit times using TTVFast7 in combination with the emcee8 implementation of the Affine Invariant MCMC Ensemble sampler54. For each planet, we parameterize the pair of eccentricity e and argument of periastron ω with the pair of ecosω and esinω at the start of the TTVFast simulation. We furthermore fit the initial transit time t0 of the orbit at the start of the TTVFast run in place of the mean anomaly M itself because the initial transit time describes the position of the planet equivalently to M, but is much less correlated with ω, thereby facilitating the convergence substantially. Our set of ecosω, esinω and t0 for each planet is equivalent to the set of e, ω and M. We do not include free parameters for planet b in our TTV analysis because the predicted amplitude of the TTVs for planet b are below one second, independent of the masses of planets c and d.

Using this setup, we compare two TTV analyses with different choices for the eccentricity prior. The first analysis uses a non-informative eccentricity prior on ecosω and esinω (refs. 3,55), whereas the second analysis takes into account that tidal damping in the LP 791-18 system should have dampened the free eccentricities of the planetary orbits56 on timescales short compared to the age of the system (Extended Data Fig. 3). This does not mean that the overall eccentricities of the planets are zero. Instead, tidal damping in the LP 791-18 system should only have dampened the free eccentricities, whereas a significant forced eccentricity on LP 791-18d can be preserved due to the mutual interaction between LP 791-18c and d (ref. 56) (Extended Data Fig. 3). We implement this tidally damped-state prior on the free eccentricities by first computing the free and forced eccentricity components for planets c and d for each proposed set of MCMC fitting parameters and then imposing Gaussian priors on the values of the free eccentricities centred at zero and with a standard deviation of 0.001. The result is a tidally damped-state prior that effectively constraints the fits to systems with near-zero free eccentricities without enforcing zero overall eccentricity at the initialization of the TTVFast simulation. The free and forced eccentricity components are calculated numerically by running rapid N-body integrations of the LP 791-18 system for each proposed set of MCMC parameters using the REBOUND library57,58 and fitting a circle to the eccentricity vectors found by the N-body integration over time. The centre of this circle represents the free eccentricity of the planet, whereas the circle radius represents the forced eccentricity of the planet56. We use the WHFast integrator, 1 × 104 time steps per orbit of the closest planet, and simulate the orbits for 2 years, which is sufficient to capture many of the 26-day super-periods of planets c and d. In addition, in all TTV analyses, we include a Gaussian prior for the stellar mass as listed in Extended Data Table 3, and we fix the inclination to the results from the joint light-curve fit and the longitude of the ascending node to π/2. We use uniform priors for the planet masses.

We find that both TTV analyses, with and without the tidally damped-state prior, provide adequate fits to all 72 transit timing measurements and consistent planet masses. A marginally better fit is obtained in the analysis without the tidally damped-state prior, which allows for non-zero free eccentricities (χ2/N = 0.92). However, given that the TTV analyses with tidally damped-state prior also adequately fits all 72 transit timing measurements (χ2/N = 1.1) and given that the tidal circularization timescale is short compared to the age of the system (Extended Data Fig. 3), we report the results from the TTV analyses with tidally damped-state prior in Extended Data Table 4. We then conservatively use only the forced eccentricity component, directly introduced by planet c, when calculating the tidal heating rate for LP 791-18d (Fig. 3). If any free eccentricity existed in the system, this would additionally increase the tidal heating rate for LP 791-18d.

Finally, we double check that the TTV solutions are not affected by any potential outliers in the mid-transit timing measurements. For that, we make eight repeats of the TTV analyses. Four repeats use all measured mid-transit times listed in Extended Data Tables 1 and 2 (A1–A4), whereas the other four repeats (B1–B4) explicitly exclude transits with relatively lower SNR or short pre- or post-transit baselines (Observations d2, d3, d9, d15, d17, d36, d38 and c21). The four separate TTV analyses for each set (A and B) are then performed using four different likelihood models. The first likelihood model assumes standard Gaussian uncertainties with the nominal error bars directly taken from Extended Data Tables 1 and 2 (Analyses A1 and B1). The second likelihood model also assumes Gaussian noise, but additionally includes an uncertainty scaling factor V1 (analyses A2 and B2). The third likelihood model explicitly accounts for a possibly wider tail in the mid-transit timing uncertainties using a Student’s t-distribution with two degrees of freedom for the observational uncertainties (ν = 2)59 (analyses A3 and B3). Finally, the fourth likelihood model uses the most general form of the Student’s t-distribution simultaneously fitting both the uncertainty scaling factor log(V1) and as well as the degrees of freedom ν (ref. 3) (analyses A4 and B4). For the last two cases, the log likelihood function of the Student’s t-distribution for each data point i is given by

$$\log {{\mathcal{L}}}_{i}(\theta ,\nu ,{V}_{1})=\frac{\nu +1}{2}\log \left(1+\frac{{({t}_{{\rm{o}}{\rm{b}}{\rm{s}},i}-{t}_{{\rm{m}}{\rm{o}}{\rm{d}}{\rm{e}}{\rm{l}},i}(\theta ))}^{2}}{\nu {\sigma }_{i}{V}_{1}}\right)-\frac{1}{2}\log (\pi \nu {V}_{1})+\log \varGamma \left(\frac{\nu +1}{2}\right)-\log \varGamma \left(\frac{\nu }{2}\right),$$
(2)

where Γ(x) is the Gamma function, tobs,i are the observed mid-transit times and tmodel,i(θ) are the mid-transit times predicted by the model for a given set of planet and orbital parameters θ. The total log likelihood is obtained by summing all the log likelihood values for the individual data points. We perform repeated emcee runs from widely different starting conditions, and we use up to 880 walkers (80 walkers per fitting parameter) and 15,000 steps, many times beyond the formal convergence criterion. We obtain consistent results for all eight independent analyses (A1–B4). In particular, the inferred planet masses and orbital eccentricities of planets c and d agree within their uncertainties.

Note that during our entire work, we exclude one MEarth-N transit of planet d taken 8 February 2020 (Exoplanet Follow-up Observing Program (ExoFOP) tag ID 16501) as this transit is incomplete, an LCOGT observation taken on 17 March 2020 (tag ID 18144) affected by clouds passing during pretransit, as well as one SPECULOOS South transit of planet d taken on 4 March 2020, which was affected by systematics in the light curve and disagreed with the four transit times obtained with MuSCAT2, MEarth-S, TRAPPIST-N and LCOGT-CTIO observation during the same night.

Tidal damping analysis

To investigate the tidal damping of free eccentricities in the LP 791-18 system, we perform N-body integrations using the symplectic Wisdom–Holman integrator WHFast with tidal heating implemented in the REBOUNDx libraries57,58,60. We use the masses of planet c and d as inferred in the TTV analysis and assume an Earth-like iron-rock composition for planet b (Mb = 1.8 M⊕). We then initiate the orbits of the three planets with the three semimajor axes inferred from the planets’ measured orbital periods (Extended Data Table 4) and deliberately impose substantial initial free eccentricities between 0.02 and 0.05. The N-body integration then models the evolution of the three orbits due to tidal damping and the planets’ mutual gravitational interaction. We find that the free eccentricities are rapidly damped over timescales short compared to the age of the system (Extended Data Fig. 3). This is true even when the tidal quality factors is significantly increased above the generally assumed values of Qp = 10–100 for terrestrial planets61. We find that the dynamical evolution remains rapid and qualitatively similar to Extended Data Fig. 3 even for tidal quality factors of Qp = 1,000 for LP 791-18b and LP 791-18d or a Neptune-like tidal quality factor of Qp = 2 × 105 for the sub-Neptune LP 791-18c. We note, however, that despite the tidal damping, a significant non-zero forced eccentricity circulating around 0.0015 is preserved for LP 791-18d.

System stability analysis

We perform N-body integrations of the LP 791-18 system using the REBOUND library57,58, choosing the symplectic Wisdom–Holman integrator WHFast. As a conservative approach, we choose the highest allowed masses and eccentricities within error bars for planets c and d. The eccentricity of planet b is not observationally constrained; however, assuming an effective rigidity \(\widetilde{\mu }={\left({10}^{4}{\rm{km}}/{R}_{{\rm{p}}}\right)}^{2}\), a tidal quality factor Qp = 100, and a planet mass of Mb = 1.8 M⊕ for a Earth-like iron-rock composition, we argue that the tidal circularization timescale of planet b62

$${\tau }_{{\rm{e}}}=\frac{4}{63}\frac{\mathop{\mu }\limits^{ \sim }{Q}_{{\rm{p}}}}{2\pi }\frac{{M}_{{\rm{p}}}}{{M}_{\ast }}{\left(\frac{a}{{R}_{{\rm{p}}}}\right)}^{5}P$$
(3)

is only τe of roughly 4.2 × 104  years and much shorter than the age of the system. For the N-body integrations, we therefore initialize planet b’s orbit with an eccentricity near zero (0.01) and take the semimajor axis a and Rp of planet b from Extended Data Table 4. We furthermore assume zero inclination for all objects for the N-body integrations. We integrate the system for 109 orbits of planet c, with a time step of 0.1 days. This timescale is long enough to allow for secularly driven and chaotic diffusive instabilities to manifest if present. We run ten simulations with random initial anomalies and arguments of periapsis, and find them all to be stable with no extreme eccentricity excitation for any object. An example simulation is shown in Extended Data Fig. 4a,b.

Stability of LP 791-18 with hypothetical additional planets

To assess whether the system can dynamically accommodate a fourth unseen planet, we run a suite of N-body integrations with one additional hypothetical planet introduced on a circular orbit in each simulation. Across the simulations, the semimajor axis of the hypothetical planet ranges between 0.015 and 0.045 astronomical units (AU), that is, we consider a wide range of orbits from interior to LP 791-18d to orbits exterior to the outermost planet LP 791-18c. Representative scenarios with a hypothetical 1 M⊕ planet at different locations in the system are shown in Extended Data Fig. 4c–h. The system stability simulations are performed as before, but using the higher-order IAS15 integrator available in the REBOUND library. We find that the system can accommodate a 1 M⊕ planet with semimajor axes near 0.015 AU (between planets b and d) without triggering dynamical instability (Extended Data Fig. 4c,d). Similarly, a planet in an orbit sufficiently outside planet c can be stable (Extended Data Fig. 4e,f). On the other hand, any planet orbiting between planet d and c or any planet orbiting too closely exterior of planet c (for example, at 0.035 AU) will quickly make the system unstable, with either planet d or the fictional planet being ejected (Extended Data Fig. 4g,h). These findings are equivalent for hypothetical planets with substantially lower mass (0.1 M⊕) or higher mass (2 M⊕).

Interior modelling and susceptibility to mass loss

We interpolate over a grid of interior models with Earth-like core compositions and solar-composition hydrogen envelopes9 to estimate the maximum amount of hydrogen that could be present on LP 791-18d today63. We take into account the present-day insolation of LP 791-18d and conservatively assume a stellar age of 10 Gyr because any gas envelopes, if present, would shrink as the planet cools with age. We find that even the lowest hydrogen-mass fraction in the grid (0.01%) corresponds to a radius of 1.23 R⊕, whereas LP 791-18d has a radius of only 1.03 ± 0.04 R⊕ (Extended Data Fig. 5). We therefore take 0.01% as a conservative upper limit on the amount of hydrogen that can at present be accommodated by the measured planet parameters. The long-term stability of such a hypothetical low-mass hydrogen-dominated envelope of less than 0.0001 M⊕ is, however, put into question from basic atmospheric escape considerations. We estimate hydrogen-mass-loss rates for hydrostatic Jeans escape as well as hydrodynamic energy-limited escape, and find in both cases that even the highly conservative 0.01% hydrogen envelope would be quickly lost on timescales of 10–500 Myr.

For Jeans escape, we use equation 1 from ref. 64. to estimate the escape flux for various particle number densities and temperatures nexo and Texo at the exobase. We find envelope loss timescales \({\tau }_{{\rm{esc}}}={M}_{{\rm{env}}}/{\dot{M}}_{{\rm{env}}}\) of the order of 10–100 Myr for nexo similar Earth or Jupiter65,66, with the exact value depending on the assumed exobase altitude and temperature at the exobase67. If the upper atmosphere were puffed up by absorption of high-energy stellar radiation63, the high altitude of the exobase and larger kinetic energy of atmospheric particles would further loosen the particles’ gravitational binding and make the atmosphere even more susceptible to escape. Equivalently, we estimate an escape flux for hydrodynamic energy-limited escape:

$$\dot{M}=\eta \frac{\pi \,{R}_{{\rm{p}}}\,{R}_{{\rm{e}}{\rm{f}}{\rm{f}}}^{2}{L}_{{\rm{H}}{\rm{E}}}}{4\pi {a}^{2}G\,{M}_{{\rm{p}}}}f(A)$$
(4)

where η is the mass-loss efficiency (η < 1 to accounts for energy losses), Rp is the planet radius, Reff is the effective radius of the photosphere at extreme ultraviolet (XUV) wavelengths that can reach several times Rp, LHE is the star’s high-energy luminosity, a and Mp are the semimajor axis and mass of the planet, and the factor f(A) (roughly 1.04 to 1.07) accounts for the enhanced atmospheric mass loss in the presence of stellar flares14,68. Our prescription for the high-energy luminosity LHE is the same as in previous work69, with a constant luminosity for the first 100 Myr and a logarithmic decay over the rest of the star’s lifetime14,70,71,72,73. We use η = 10%, appropriate for super-Earths and sub-Neptunes74. We derive atmosphere loss timescales for Reff = 1 to 2Rp of 30–200 Myr for a 1 Gyr old star or 100–600 Myr for a 10 Gyr old star for the conservatively assumed 0.01% hydrogen envelope.

For the sub-Neptune LP 791-18c, we perform a Bayesian analysis to constrain its composition using the open-source smint69 tool and the model grid from ref. 9. We find a hydrogen-mass fraction of \({2.0}_{-0.5}^{+0.6} \% \) to match observed radius for a core with Earth-like composition (Extended Data Fig. 5). Such a massive hydrogen envelope could be maintained over Gyr timescales on LP 791-18c.

Testing consistency with models of photoevaporation and core-powered mass loss

We use the ratio of the mass-loss timescales of LP 791-18c and LP 791-18d to assess whether the planet pair is consistent with the predictions from both the photoevaporation14,75 and core-powered mass-loss models15,76 as possible explanations for the origin of the radius valley11. In both models, the initial condition is assumed to be a population of planets with H or He envelopes, out of which the planets that eventually end up below the radius valley lose their envelopes by means of thermal escape either driven by XUV heating from the host star (photoevaporation) or driven by the planetary core’s own cooling luminosity (core-powered mass loss). Systems with several transiting planets are well-suited for testing these models by means of mass-loss timescales arguments because the poorly constrained XUV and bolometric luminosity histories of the host star cancel out when computing the ratio of the mass-loss timescales of two planets orbiting the same star. LP 791-18c and d is a special pair because it is the first time that the photoevaporation and core-powered mass-loss models are tested for planets orbiting a late-M dwarf, and in addition in orbits with low equilibrium temperatures. We thus compute the ratios of the mass-loss timescales of LP 791-18c and d as

$$\frac{{t}_{{\rm{loss}},{\rm{c}}}}{{t}_{{\rm{loss}},{\rm{d}}}}=\frac{{\left({M}_{{\rm{c}}}/{M}_{\oplus }\right)}^{0.64}}{{M}_{{\rm{d}}}/{M}_{\oplus }}{\left(\frac{{a}_{{\rm{c}}}}{{a}_{{\rm{d}}}}\right)}^{2/3}{\left({R}_{{\rm{d}}}/{R}_{\oplus }\right)}^{4/3}$$
(5)

for the photoevaporation model17,75 and as

$$\frac{{t}_{{\rm{loss}},{\rm{c}}}}{{t}_{{\rm{loss}},{\rm{d}}}}=\frac{{M}_{{\rm{c}}}}{{M}_{{\rm{d}}}}{\left(\frac{{T}_{{\rm{eq}},{\rm{c}}}}{{T}_{{\rm{eq}},{\rm{d}}}}\right)}^{-3/2}{\rm{\exp }}\left[c{\prime} \left(\frac{{M}_{{\rm{c}}}}{{T}_{{\rm{eq}},{\rm{c}}}{R}_{{\rm{c}}}}-\frac{{M}_{{\rm{d}}}}{{T}_{{\rm{eq}},{\rm{d}}}{R}_{{\rm{d}}}}\right)\right]$$
(6)

for the core-powered mass-loss model15,17,76. Here, M is the planet mass, a is the orbital semimajor axis, R is the planet radius and Teq is the equilibrium temperature, with the indices indicating planet c or d. The constant \(c{\prime} \) is approximately equal to \({10}^{4}{R}_{\oplus }{\rm{K}}{M}_{\oplus }^{-1}\). Several assumptions were made in the derivation of equation (5) including that the mass-loss efficiency under the photoevaporation model is antiproportional to the square of the escape velocity14, that the planet cores have Earth-like compositions and that the planet masses are dominated by the core masses. In addition, for the core-powered mass-loss model, equation (6) assumes that most of the atmospheric gas lies within its convective zone and that the radius at the radiative–convective boundary is equal to the measured planet radius17. Using equations (5) and (6), we plot the posterior distributions of the mass-loss timescale ratios for LP 791-18c and d under the models of photoevaporation and core-powered mass loss in Extended Data Fig. 6. We find that the pair of the sub-Neptune LP 791-18c and the Earth-sized planet LP 791-18d is consistent with both the models of photoevaporation and core-powered mass loss for all planet masses, radii and semimajor axis consistent with observational uncertainties.

Tidal synchronization

We investigate whether LP 791-18d is tidally locked by computing its tidal synchronization timescale τsyn (ref. 77) and comparing it to the lower limit on the LP 791-18 system’s age of 500 Myr (Extended Data Table 3). Owing to LP 791-18d’s small semimajor axis and short orbital period, we find that the tidal synchronization timescale is much shorter than the system’s age for all plausible values of the tidal quality factor Q. For Qp = 10–100 characteristic of rocky planets61, we obtain τsyn equal to only 3–30 years corresponding to a few thousand orbital periods. Even for a Qp = 106.5 typical of gaseous planets78, we would obtain 1 Myr for the tidal synchronization timescale, which remains orders of magnitude shorter than the lower inferred limit on the system’s age. Finally, the possibility of capture into a higher spin-orbit resonance is also extremely unlikely due to the strong dissipative tidal torque exerted on the planet for an orbit as compact as that of LP 791-18d (ref. 79). Similarly, thermal tides in the atmosphere are unable to significantly affect the spin of a planet this close to a low-mass star80. We conclude that the planet is extremely likely to be tidally locked in a spin-orbit synchronous resonance.

Tidal heating model

We use the tidal heating model previously applied to the interior of Io81,82,83,84 and the TRAPPIST-1 planets85, as implemented within the open-source tool melt. Assuming that the planet is in synchronous rotation, we calculate its tidal energy dissipation as:

$${\dot{E}}_{{\rm{tidal}}}=-\frac{21}{2}{\rm{Im}}\left({k}_{2}\right)\frac{{R}^{5}{\omega }^{5}{e}^{2}}{G},$$
(7)

where R and e are the planet’s radius and orbital eccentricity, Im(k2) is the imaginary part of the planet’s Love number, G is the gravitational constant and ω is equal to 2π/P with P being the orbital period86. Instead of using a fixed tidal quality factor Q to assess the rate of energy dissipation per tidal cycle, we adopt the Maxwell model of viscoelastic rheology to take into account the feedback between the thermal state of the planet’s interior and its response to tidal forcing. In the Maxwell model, Im(k2) is evaluated as:

$${\rm{Im}}({k}_{2})=-\frac{57\eta \omega }{4\bar{\rho }gR\left[1+{\left(1+\frac{19\mu }{2\bar{\rho }gR}\right)}^{2}\frac{{\eta }^{2}{\omega }^{2}}{{\mu }^{2}}\right]}$$
(8)

where η is the viscosity of the material, μ is the shear modulus, \(\bar{\rho }\) is the average density of the planet and g the surface gravity of the planet81,82,83,84,85.

We then obtain the mantle equilibrium temperature Tmantle as the temperature for which the globally averaged tidal heat flux \({F}_{{\rm{t}}{\rm{i}}{\rm{d}}{\rm{a}}{\rm{l}}}={\dot{E}}_{{\rm{t}}{\rm{i}}{\rm{d}}{\rm{a}}{\rm{l}}}/4\pi {R}^{2}\) is in balance with the rate of radial energy transport towards the surface by means of convection Fconv (refs. 85,87,88), that is, satisfying:

$$\frac{{\dot{E}}_{{\rm{t}}{\rm{i}}{\rm{d}}{\rm{a}}{\rm{l}}}({T}_{{\rm{m}}{\rm{a}}{\rm{n}}{\rm{t}}{\rm{l}}{\rm{e}}})}{4\pi {R}^{2}}=0.53{\left(\frac{{Q}^{\star }}{{R}_{{\rm{G}}}{T}_{{\rm{m}}{\rm{a}}{\rm{n}}{\rm{t}}{\rm{l}}{\rm{e}}}^{2}}\right)}^{-4/3}{\left(\frac{\rho g\alpha {k}_{{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}{\rm{m}}}^{3}}{{\kappa }_{{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}{\rm{m}}}\eta ({T}_{{\rm{m}}{\rm{a}}{\rm{n}}{\rm{t}}{\rm{l}}{\rm{e}}})}\right)}^{1/3}.$$
(9)

Here, RG is the universal gas constant, and the properties of rock are used for the activation energy Q⋆ = 333 kJ mol−1, the coefficient of thermal expansion α = 3 × 10−5 K−1 and the thermal diffusivity κtherm = ktherm/(ρCp) with ktherm = 3.2 W m−1 K−1 and Cp = 1,200 J kg−1. For the density we use ρ = 5,000 kg m−3, appropriate for a pure rock composition87. \({\dot{E}}_{{\rm{tidal}}}\) depends on Tmantle in equation (9) by means of the temperature dependence of the shear modulus μ and the viscosity η. At temperatures below the solidus of rock (Ts = 1,600 K), we use μ = 50 GPa and \(\eta \left(T\right)={\eta }_{0}\exp \left({Q}^{\star }/\left({R}_{{\rm{G}}}T\right)\right)\) with η0 = 2.13 × 106 Pas (refs. 81,83). Between the solidus temperature and the ‘breakdown point’ (Tb = 1,800 K), which marks the transition to a regime in which the shear stiffness becomes negligible89, we use the shear modulus \(\mu \left(T\right)={10}^{\frac{{\mu }_{1}}{T}+{\mu }_{2}}\) where μ1 = 8.2 × 104 K and μ2 = −40.6. The viscosity in this regime is described as \(\eta \left(T\right)={\eta }_{0}\exp \left({Q}^{\star }/\left({R}_{{\rm{G}}}T\right)\right)\exp \left(-Bf\right)\), where the melt fraction coefficient B describes the dependency of the rock viscosity on the melt fraction f and experimentally constrained to be between 10 and 40 (ref. 82). The melt fraction f, in turn, increases linearly from 0 to 0.5 between Ts and Tb (refs. 81,82).

For LP 791-18d, specifically, we compute the equilibrium mantle temperature and the corresponding tidal heat flux using the median parameters in Extended Data Table 4. We explore the full range of experimentally determined values for the melt fraction coefficient B of rock between 10 and 40 (ref. 82). We find that, as LP 791-18d cooled down, equilibrium occurred for T > Ts for all values of B, which is a stable equilibrium82,84. The corresponding tidal flux at the planet’s surface is 0.2–0.9 W m−2 depending on the exact value of melt fraction coefficient (Fig. 3). Surface volcanic eruptions are an expected consequence of the tidal heating if the rocky mantle reaches up to the planetary surface. The tidal heating thus probably results in the presence of permanent molten magma over the lifetime of the system, with volcanic activity potentially similar to that on Jupiter’s volcanically active moon Io5,6.

Spitzer sensitivity tests

To determine whether additional transiting planet could exist without being detected in the Spitzer light curve, we perform a suite of injection-and-recovery tests. First, we evaluate the sensitivity of the Spitzer observations to small planet between planets b and d. We generate 180,000 transit signatures for planets with radii randomly distributed between 0.5 and 1.0 Earth radii, transit impact parameters randomly distributed between 0 and 0.8, and orbital periods randomly sampled from a log-uniform distribution between 0.5 and 2.4 days. We then inject these simulated transit signatures into the Spitzer light curve at four random phases, one at a time, and measure the χ2 improvement of the transit model versus a straight line on the injected light curve. In total, this results in 720,000 injections and χ2 values. We then randomly selected 6,000 of these injections and run a transit recovery search on them. We model the recovery rate as a function of the χ2 improvement of the injected signals and use this to calculate a theoretical recovery rate for each signal. These rates are then binned by period and radius to determine which sizes of planets could be missed in the Spitzer data at different orbital periods. We conclude that any transiting planets between planets b and d with radii larger than roughly 0.8 R⊕ should have been detected by the Spitzer observations with a probability greater than 90%.

In a separate analysis, we furthermore investigate the sensitivity of the Spitzer photometry to single-transit events. We find that any single transit of a planet larger than 1.2 R⊕ should have been detected at a probability greater than 95%. As we detect no additional single-transit event in the data, we conclude that such transiting planets in longer periods either do not exist or did not transit during the 127 h (5.3 days) we observed. Assuming random orbital phase, our detection fraction for planets larger than 1.2 R⊕ outside the orbit of planet c is therefore simply the amount of time observed (5.3 days) divided by the period of the hypothetical planet.

Discussion of LP 791-18d’s climate state

3D global climate models predict the possibility of two stable climate regimes for Earth-sized planets such as LP 791-18d near the inner edge of the habitable zone, resulting from a competition between the greenhouse effect and the condensation of the greenhouse gases H2O and CO2 on the cold night side22. LP 791-18 may have entered a Venus-like runaway greenhouse state20,21. In this regime, the tidally locked planet could initially have formed a thick layer of highly reflective clouds at the permanent substellar point20,90, which would have lowered the globally averaged equilibrium temperature to near 300 K for a Venus-like albedo. However, in this regime, large amounts of water could still have been lost to space over the lifetime of the system, plausibly leaving the planet dry. Alternatively, if the initial heat redistribution to the night side was weak, LP 791-18d’s atmosphere could have entered a ‘collapsed’ regime, with water being captured in permanent cold traps on the night side or near the poles22,23. As more of the greenhouse gases condensed, the atmosphere would have cooled down further, thereby accelerating the condensation. The result could be a thick ice cap on LP 791-18d’s night side. Temperatures would probably be too low for liquid surface water on the night side; however, the considerable geothermal flux (Fig. 3) combined with high pressures reached at the bottom of the ice caps could result in subsurface liquid water22. A sufficiently thick ice cap on the night side could then plausibly also trigger gravity-driven glacial ice flows transporting ice towards the warmer regions near the terminator where it could melt to form liquid surface water22.

Prospects for future atmospheric characterization

So far, the planets in the TRAPPIST-1 system are the only temperate (lower than 400 K) Earth-sized planets approved for substantial James Webb Space Telescope (JWST) observations for spectroscopic follow-up studies. However, there remains a possibility that all the TRAPPIST-1 planets have a common formation and evolution history3, which may have left the system volatile-poor and the planets bare without atmospheres. LP 791-18d presents a powerful opportunity to spectroscopically study a temperate Earth-sized planet outside the TRAPPIST-1 system, in particular in a system where at least one planet (LP 791-18c) accreted and retained a substantial amount of gas and volatiles. From an observational perspective, LP 791-18’s small stellar radius (0.182 ± 0.007 R⊙) and extremely low stellar luminosity (0.00230 ± 0.00001 L⊙) make LP 791-18d an exceptional M star opportunity, especially because the stellar radius shrinks rapidly beyond spectral type M4-51. The observable transit depth contrast between inside and outside atmospheric absorption bands in LP 791-18d’s transmission spectrum should be as high as 30–100 ppm even for compact high-mean molecular-weight terrestrial atmospheres, such as CO2-dominated, N2-dominated or H2O atmospheres, despite the planet’s small size and low temperature (Fig. 4). Such transit depth contrasts across the spectrum are well above the expected systematic noise floor of JWST instruments27 and LP 791-18d’s high Transit Spectroscopy Metric26 combined with frequently occurring transit events allows for efficient exploration of LP 791-18d’s atmosphere, its climate state and possibly its planetary geochemistry.