Coherent manipulation, measurement and entanglement of individual solid-state spins using optical fields

Abstract

Realization of a quantum interface between stationary and flying qubits is a requirement for long-distance quantum communication and distributed quantum computation. The prospects for integrating many qubits on a single chip render solid-state spins promising candidates for stationary qubits. Certain solid-state systems, including quantum dots and nitrogen–vacancy centres in diamond, exhibit spin-state-dependent optical transitions, allowing for fast initialization, manipulation and measurement of the spins using laser excitation. Recent progress has brought spin photonics research in these materials into the quantum realm, allowing the demonstration of spin–photon entanglement, which in turn has enabled distant spin entanglement as well as quantum teleportation. Advances in the fabrication of photonic nanostructures hosting spin qubits suggest that chips incorporating a high-efficiency spin–photon interface in a quantum photonic network are within reach.

Main

Due to their insensitivity to electrical noise, spin degrees of freedom are widely considered to be promising candidates for storing information^1,2,3. To operate a confined spin as a memory element for quantum information, it is essential to fully controllably turn on and off its coupling to external charge or electromagnetic degrees of freedom so that quantum information can be reliably written or read out. The spin–orbit interaction plays a crucial role in this endeavour, either by providing means for direct electrical manipulation of spins or by enabling spin-dependent optical transitions where different spin-states couple to light fields with different polarization or frequency (Box 1). Of particular interest is the realization of a spin–photon quantum interface^4,5,6,7. In this Review, we primarily focus on recent advances that use quantum entanglement between a confined spin and a propagating photon to demonstrate basic quantum information protocols between distant qubits^8,9,10.

To generate a spin–photon quantum interface, spin–orbit interaction is only required to be strong in the optically excited state. As thermal excitation to the optically excited states is completely negligible, the spin remains isolated from its environment unless a laser field is applied. It should be emphasized that incoherent optical manipulation of spin ensembles is not new and has been extensively used by physicists and chemists alike in optical pumping, dynamical nuclear spin polarization and Kerr rotation experiments since the 1950s. More recently, motivated by potential applications in quantum information processing, a promising research direction investigating quantum coherent optical manipulation and measurement of individual isolated spin qubits has emerged. When the individual spins are embedded in a solid-state matrix, nanofabrication techniques enable the integration and control of qubits on chips, potentially paving the way for a scalable quantum information processing architecture^2,11,12,13.

Although various promising approaches to scalable quantum computation are being actively pursued, quantum communication research has been exclusively based on the use of single-photons as flying qubits carrying quantum information over long distances. For this application, the availability of a quantum interface between stationary qubits and flying photonic qubits in well-defined optical modes is crucial^{4,5,6,7,8,9,10,14,15,16,17}. In addition to implementing long-distance quantum-state transfer or quantum teleportation, interfacing stationary qubits with single photons could be used to connect few-qubit nodes in a quantum network¹⁶. Here we review the rapid progress in the emerging field of spin photonics, where the overarching goal is the realization of a spin–photon quantum interface as well as the implementation of coherent optical manipulation and measurement of solid-state spins.

Experimental research in spin photonics has so far focused primarily on optically active quantum dots (QDs) and nitrogen–vacancy (NV) centres in diamond. In the first section of this Review we discuss the recent achievements as well as the limitations of efforts aimed at using QDs. QDs stand out for their superior optical properties and benefit directly from advanced semiconductor nanotechnology, but suffer from relatively short spin coherence times. In contrast, the spins in NV-centres, which we describe in the second section of this Review, have remarkable spin coherence and yet suffer from low yield on coherent light scattering. Of particular common interest for these two systems is the exploitation of a unique feature of the solid-state approach—the possibility of shaping the solid-state host in which the spins are embedded into a photonic nanostructure incorporating cavities and waveguides, which not only enhance the spin–photon coupling strength but also ensure high collection efficiency of the generated photons. However, the advantages of a solid-state approach are by no means unique to QDs and NV centres. In the third section we briefly review emerging spin photonics systems such as colour centres in other wide-bandgap materials such as SiC and spin degrees of freedom in rare-earth-ion doped crystals. In the last section, we present the outstanding challenges and future prospects.

Box 1: Basic requirements and potential systems for spin photonics.

The essential requirements for implementation of a solid-state spin–photon interface are (1) the presence of an impurity or an island in a solid-state matrix with a degenerate ground-subspace stemming from spin degrees of freedom, and (2) an optical transition to excited states that exhibits strong spin–orbit coupling. The latter condition ensures that the scattered photons are correlated with the final spin state.

There are three classes of emitters that are relevant for spin photonics: the first class comprises defects or islands where the relevant quasiparticles, such as electrons and holes, have elementary properties, such as effective mass and g-factor, that are similar or identical to those of the host solid-state matrix. Examples for emitters that are in this category include practically all single-electron or hole-charged optically active QDs as well as shallow-impurity-bound excitons in semiconductors. The spin confinement length scale for these emitters is typically comparable to the Bohr radius of the host, and as such, is much larger than the lattice constant. The second class of emitters includes deep defects or colour centres in wide-bandgap insulators. In this class, the properties of relevant quasiparticles and the optical selection rules can be drastically different than those of the host and of the impurity atoms. The confinement length scale for these emitters is typically a few lattice constants. The best-known example for emitters in this category are NV centres in diamond.

The third class of emitters are based on optical transitions of f- or d-shell electrons of impurity atoms or ions, which are shielded from the host by the outer electron shell. The electronic properties in this case stem primarily from the impurity and the confinement length scale is essentially identical to that of an isolated ion. Emitters based on rare-earth ions in crystals are in this category.

Quantum dots

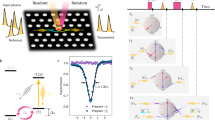
QDs are mesoscopic semiconductor structures that confine the motion of the electron and/or hole in all three dimensions. Electrically defined QDs offer a high degree of tunability and high-fidelity electrical control of spins^1,18. However, gate voltages that confine the conduction-band electrons repel the valence-band holes from the QD, challenging the prospects for obtaining discrete atom-like optical spectra. Consequently, QD-based spin photonics research has focused almost exclusively on self-assembled InGaAs QDs embedded in a GaAs matrix (Fig. 1a), which allows for simultaneous quantum confinement of both electrons and holes and exhibits discrete optical spectra^19,20. Whereas predetermination of the spatial position and the resonance frequency of QDs is an active and promising research direction²¹, the majority of the results in spin photonics have been obtained using samples where the QD ensemble has a large inhomogeneous broadening and QDs appear at random sites during molecular-beam-epitaxy growth.

Figure 1: Quantum dot spin initialization, detection and manipulation.

a, Cross-sectional transmission electron microscopy micrograph of a single InGaAs/GaAs quantum dot. Reproduced from ref. 126, APS. b, Resonance fluorescence from a negatively-charged quantum dot trion state shows that approximately 90% of the photons are emitted at the ZPL. The data is measured with a spectrometer when the laser is on resonance with the trion state. The plot shows the counts in logarithmic scale as a function of the emission wavelength. c, The energy level diagram with a magnetic field, B_x, applied parallel to the sample surface (Voigt geometry). In this configuration, both spin states, |↑〉 and |↓〉, are coupled equally strongly to the two excited states, |T_b〉 and |T_r〉, with horizontal (H) and vertical (V) polarizations. d, Simplified model for spin initialization. Initially the spin population is equal for the |↑〉 and |↓〉 states. The spin can be optically prepared in |↓〉 with high fidelity after several excitation and decay cycles with a resonant laser (black arrow) driving the |↑〉 ↔ |T_b〉 transition. e, Spin measurement. Photon detection events will reveal that the spin is in the |↑〉 state when a resonant laser drives the |↑〉 ↔ |T_b〉 transition. f, Spin rotation along the latitude on the Bloch sphere. A 2π-detuned laser (black arrow) with horizontal polarization induces a different geometric phase to |↑〉 and |↓〉, which will constitute a spin rotation (red arrow) along the latitude on the Bloch sphere, similar with the effect of Larmor precession. g, Spin rotation along the longitude on the Bloch sphere. An off-resonant σ⁺ polarized laser field (black arrows), with a detuning of Δ, coupling to double Λ-type transitions rotates spin along the longitude (red arrow) on the Bloch sphere.

Properties of optically active QDs. The radiative efficiency of the fast optical transitions in InGaAs QDs is close to unity, with approximately 90% of the photons emitted in the zero-phonon line (ZPL) (Fig. 1b). For QDs in high-quality samples, spontaneous-emission-broadened resonance linewidths have been measured at 4 K. Demonstration of indistinguishability in a Hong–Ou–Mandel (HOM) two-photon interferometer provides direct evidence that the input photons are in a pure quantum state with identical spatiotemporal profiles. Two perfectly indistinguishable single-photon pulses incident on a HOM interferometer will never lead to a coincidence detection event at the output. Two successive photons from a single QD have been shown to yield a normalized coincidence rate of 0.005 (ref. 22). Arguably, what is more relevant for applications in quantum information processing is the indistinguishability of photons generated by different QDs^23,24. Local fine-tuning of QD resonance energies has recently yielded a normalized coincidence rate of approximately 0.1 (refs 8,25). This high degree of indistinguishability demonstrates that probabilistic quantum information protocols relying on the detection of a coincidence at the HOM output can be realized with QD single photons. By exclusively using coherently scattered (Rayleigh) photons in synthesized waveforms, it is possible to achieve an arbitrarily high degree of indistinguishability, albeit at the cost of photon generation efficiency²⁶.

Unlike atoms or atom-like emitters in the solid-state, the charging state of the QD can be efficiently controlled by gates²⁰. When the gate voltage ensures deterministic charging of the QD with a single excess electron, the ground-state manifold is spanned by the spin states of this electron. The optical excitation spectra in this limit is remarkably simple and exhibits strong correlations between the initial electron spin state and light polarization, which can be used for generating a spin–photon interface.

Quantum dot spin initialization, manipulation, read-out, and spin coherence. We consider a QD in a Voigt geometry, where an external field is applied perpendicular to the sample growth direction. In this configuration, both spin states, |↑〉 and |↓〉, are coupled equally strongly to the two excited states, |T_b〉 and |T_r〉 (Fig. 1c). A simplified model of the spin-pumping procedure is illustrated in Fig. 1d. When the optical transition from |↑〉 to the excited state, |T_b〉, is driven resonantly, each radiative decay event has a 0.5 probability of populating the optically dark |↓〉 state. Therefore, seven photon-scattering events will ensure preparation of the spin in the |↓〉 state with an average initialization efficiency greater than 99% within 10 ns (ref. 27).

Similarly, resonant light-scattering addressing a single spin state can be used to realize heralded spin measurements as shown in Fig. 1e. With a laser exciting the |↑〉 ↔ |T_b〉 transition, a photon detection event will indicate that the spin state is in the |↑〉 state with high fidelity. On the other hand, the absence of a photon count reveals almost no information due to the limited collection and detection efficiency. For efficient verification of the spin state, a single-shot read-out is needed^28,29. In this case, absence of counts also provides information about the spin state and a single measurement step is sufficient to read out the spin with high fidelity. In the Voigt geometry, single-shot read-out based on resonance fluorescence would require an overall photon detection efficiency, η_r, exceeding 50%. With typical values of η_r ≤ 0.01, all experiments have used heralded spin measurements requiring multiple repetitions of the experiments to verify the spin state. The required η_r for single-shot measurements can be lowered with the help of selective coupling of read-out transitions to a cavity mode³⁰, exchange-coupling to a second dot²⁸ or coupling to exciton-polaritons³¹.

Coherent rotation of the spin-state to any desired point on the Bloch sphere can be achieved using off-resonant laser pulses. Controlled spin rotations along the z axis (quantization axis) can be achieved by applying off-resonant laser pulses that temporarily shift one of the two ground-state spin levels^32,33,34 (Fig. 1f). For many experiments, ranging from implementations of spin-echo to spin-measurement in the rotated basis, coherent spin rotation along an axis perpendicular to the quantization axis is required. This rotation can be realized with an off-resonant σ⁺ laser field coupled to a double Λ-type level scheme (Fig. 1g). The origin of spin rotation could be understood either as an AC Stark shift of the spin-state in the rotated basis³⁵ or as a stimulated Raman process in the original basis³⁶. The rotation angle is proportional to the effective Rabi frequency, Ω²/Δ, where Ω is the Rabi frequency coupling to each transition and Δ represents the large laser detuning.

One key requirement for spin photonics application is long spin coherence times, ensuring that the QD spin does not interact with the environment degrees of freedom in an irreversible manner. In III–V materials, electron spins couple relatively strongly to the nuclear spins that comprise the QD through Fermi-contact hyperfine interaction. As a consequence, the coherence time is approximately 1 ns, limiting the timescale over which quantum correlations between spins and photons can be observed^{6,37,38,39,40}. As nuclear spins constitute a quasi-static bath, a simple echo sequence can be used to prolong this timescale drastically; an electron spin-echo-T₂ time exceeding 1 μs has been reported for a QD ensemble³⁹ as well as for a single QD⁴⁰. Prolonging the coherence time of the electron spin by optical control or through the measurement of nuclear spins is an active field of research. Finally, realization of a spin–photon quantum interface is by no means restricted to single electron spins, promising alternate QD spins with more than two orders-of-magnitude longer coherence times can be achieved with hole spins^41,42,43 or coupled QD spins⁴⁴, which will be discussed in 'Quantum dot spins with long coherence times'.

Spin–photon entanglement, photon-to-spin teleportation and prospects for spin–spin entanglement. A crucial step in the realization of entanglement between distant qubits in a quantum network is the demonstration of entanglement between a stationary spin and a propagating single-photon. The experimental realization of QD spin–photon entanglement has been achieved independently by three groups^5,6,7. All three experiments are based on single-electron charged quantum dots with a Λ-type energy level scheme in the Voigt geometry (Fig. 2a). From the excited trion state, spontaneous emission occurs with equal probability to the |↑〉 and the |↓〉 state while emitting an horizontal and a vertical polarized photon, respectively. The final state then exhibits maximal entanglement between spin orientation and photon polarization and frequency (colour). Typically, quantum correlations with one of these degrees of freedom need to be erased to observe the entanglement between spin and photon polarization or colour. In one of the experimental realizations, a fast temporal selection of the photon has been used to erase the colour information, and then spin–photon polarization entanglement has been measured⁵ (Fig. 2b). A recent quantum state tomography experiment has proved that the fidelity of such an entangled spin–photon state can exceed 90% (ref. 45). In a complementary experiment, photon polarization information has been erased using polarizers, and entanglement between spin and photon colour has been demonstrated⁶.

Figure 2: Quantum dot spin–photon interface.

a, The energy diagram relevant for the generation of quantum dot spin–photon entangled states. In the Voigt geometry, the decay from the trion state |T_b〉 will generate the entangled states (1/√2)(|H, ω_b〉|↑〉 + |V, ω_r〉|↓〉), where H and V represent the polarization of the single-photon pulse and ω_b and ω_r represent the colour/centre-frequency. b, Spin–photon entanglement measurement in the computational and rotated basis. The black arrows refer to the spin orientation in the computational (vertical arrows) or rotated (horizontal arrows) basis. H/V and σ⁺/σ⁻ represent the photon projection basis. Reproduced from ref. 5, NPG. c, Teleportation with two different input qubits: |ω_r〉 + |ω_b〉 and |ω_r〉 − |ω_b〉. The spin measurement basis is differentiated by column colour. The plots show three-fold coincidence counts between the two output arms of the beamsplitter and a photon detection during the following spin measurement pulse (period = 0) or during a later pulse period (period > 0). The spin fidelity in period zero indicates successful teleportation (with the case period > 0 shown for comparison). Reproduced from ref. 8, NPG. d, A scheme for generation and measurement of spin–photon entanglement in a quantum dot molecule. The transitions R₊ ↔ T₀ and R₊ ↔ S can be used to generate entangled states between a photonic colour qubit and a singlet/triplet (S/T₀) spin qubit, analogous to the case of a single spin in the Voigt geometry. An important feature of this system is that, T₊ ↔ R₊₊ is a cycling transition and can be used to achieve high fidelity spin read-out. In the depicted scheme, T₀ is first populated to R₊₊ (orange triangles) and then the cycling transition is used to read out the T₀ state.

An entangled spin–photon state can be used to realize elementary quantum communication protocols, such as the teleportation of quantum information from a propagating photonic qubit to a QD spin, as demonstrated in a recent experiment⁸. First, a single photon in a superposition of two colour states is generated using resonant excitation of a neutral dot. To teleport this photonic qubit, an entangled spin–photon state in a second dot is generated. Next, the photons from the two dots are sent to a HOM set-up. Provided that the single-photon pulses have identical spatiotemporal profiles, a coincidence detection at the output of the interferometer heralds successful teleportation. Using a measurement of the correlations in both the computational basis and the rotated basis, an average teleportation fidelity of 0.78 ± 0.03 is extracted. This experiment was based on single-photon colour qubits where the two orthogonal photonic states are distinguished by their centre frequencies, which differ by about 5 GHz. Similar to time-bin qubits⁴⁶, representing quantum information using photon states with a small energy difference should ensure resilience against dominant perturbations in optical fibres.

With an overall photon detection efficiency of η_p ∼ 10⁻³ from QDs and a repetition rate of R_QD = 10 MHz, a verified teleportation rate of R_QDη_p²η_r ∼ 10⁻² Hz has been measured (here η_r = η_p is the spin measurement efficiency). A natural extension of the quantum teleportation protocol is the probabilistic entanglement of spins confined in two distant QDs by using a pair of spin–photon entangled states and entanglement swapping⁴⁷. As a rough estimation, a detection efficiency of 6 × 10⁻³ is required to achieve QD spin–spin entanglement generation and verification with rates R_QDη_p² ∼ 3 × 10² Hz and R_QDη_p²η_r² ∼ 10⁻² Hz, respectively.

Quantum dot spins with long coherence times. Although spin-echo has been implemented in conjunction with spin–photon entanglement generation⁸ to prolong spin coherence times, it is desirable to use other spin degrees of freedom with longer coherence times. One possible avenue is to represent quantum information using a hole spin. As the energy level diagram relevant for optics as well as the corresponding selection rules are identical to those for the electron spins, almost all of the techniques developed for electron spins can also be used for hole spins^42,48,49,50. Unlike electron spins, however, the Bloch wave function of hole spins is composed of bonding atomic p orbitals with a vanishing overlap with the nuclei, leading to weaker hyperfine interaction^51,52,53,54. In the Voigt geometry, hole spin coherence times, T^*₂, ranging from 2 ns to over 200 ns have been measured^41,42,43. The large sample-to-sample variation has been attributed to enhanced sensitivity of hole spins to charge fluctuations. Unlike effective magnetic field fluctuations induced by hyperfine interaction, charge fluctuations strongly depend on the sample design and quality.

A more promising approach to prolong spin coherence is to represent a qubit using the spin states of a QD molecule^44,55 (Fig. 2d). In the case of two QD layers separated by a GaAs barrier of thickness ≤15 nm, the tunnel coupling leads to the hybridization of the electronic levels. In such QD molecules, the electronic wavefunctions could become delocalized. When the gate voltage is adjusted to ensure that each QD has one excess electron, the ground-state manifold consists of a spin singlet (S) and three triplet (T) states, which are the entangled states of two nearby electron spins⁵⁵. When a finite magnetic field, B, is applied and the gate voltage is tuned such that the exchange splitting, J, between the S and T states is a minimum, the S and T₀ states with zero spin projection along B form a solid-state counterpart of a clock transition. As linear electric and magnetic susceptibility simultaneously vanishes for this S/T₀ transition, the corresponding qubit is decoherence-avoiding and has been shown to exhibit a coherence time exceeding 200 ns (ref. 44). Finally, the two additional triplet states of a QD molecule offer further possibilities. Whereas optical transitions from the S and T₀ states are analogous to those of a single spin in the Voigt geometry, the optical transition from the other T states are cycling transitions that can be used to implement single-shot spin-state read-out (Fig. 2d).

NV centres

Optically active impurities in high-purity crystals are promising building blocks for quantum information processing, as they combine atom-like features such as a coherent optical interface and long-lived spin states with the potential scalability of solid-state devices. Much research effort has been focused on the NV centre in diamond, on which the elementary building blocks of a quantum network have been demonstrated. Very recently a number of experiments have shown individual addressing of other impurities such as rare-earth ions in solid-state crystals. We will first review experiments on the NV centre. We believe that many of the experimental techniques developed for NV centres can be directly translated to these newer, less developed impurity systems.

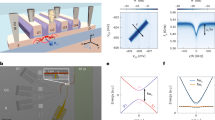
The NV centre and surrounding nuclear spins. The NV centre consists of a substitutional nitrogen atom next to an empty lattice site within the diamond lattice (Fig. 3b). In high-purity diamond crystals NV centres can be addressed individually by using standard optical confocal microscopy techniques (Fig. 3a). The two unpaired electrons of the NV centre give rise to a spin S = 1 ground-state that allows the identification of two levels that can serve as qubit states. Using magnetic resonance through the application of microwave pulses, these spin states can be coherently manipulated on nanosecond timescales^56,57 (Fig. 3d). For comparison, the electron-spin coherence time is many orders of magnitude longer (Fig. 3e). NV spin decoherence is mainly caused by magnetic interactions with (uncontrolled) surrounding spins. Therefore, reducing the number of residual spins in the environment prolongs the coherence time, which can reach milliseconds in isotopically purified diamonds³. Intriguingly, dynamically decoupling the qubit states from their environment by periodically flipping the spin can extend this time even further^58,59,60. The ultimate limit to the coherence time is yet to be explored^9,61 and is expected to be set by lattice relaxation processes that occur on a timescale of minutes at cryogenic temperatures.

Figure 3: Optical detection and spin manipulation of NV centres.

a, Single NV centres can be detected in high purity diamonds using a confocal microscope. Reproduced from ref. 81, APS. b, The electronic spin of the NV centre couples to nearby nuclear spins through the hyperfine interaction. This spin cluster can be used as a quantum register for quantum information processing. Reproduced from ref. 70, NPG. c, The hyperfine interaction leads to well-resolved spin transitions in the optically detected magnetic resonance spectrum. This spectrum is obtained by sweeping the microwave frequency while monitoring the fluorescence level of the NV centre. By tuning the microwave frequency to one of the observed transitions, the electronic spin can be manipulated conditional on the state of the surrounding nuclear spins. Reproduced from ref. 69, NPG. d, The electronic spin can be coherently manipulated by supplying microwave pulses in the GHz-frequency range to a stripline close to the NV centres (left). Reproduced from ref. 58, AAAS. By applying radiofrequency (RF) pulses in the MHz-range, coherent nuclear spin control is possible (right). P_e (0) and P_C(0) are the probabilities of finding the electron state in m_S = 0 and the nuclear state in m_I = 0, respectively. Reproduced from ref. 78, NPG. e, The coherence of the electronic spin is limited by interactions with its environment. By periodically flipping the spin it is possible to decouple it from this environment. As the number of decoupling pulses is increased the coherence time can be extended up to the milliseconds range. Reproduced from ref. 59, APS.

Although in general the spin bath surrounding the NV centre is a source of decoherence, the coupling to individual nearby spins is a valuable resource^62,63. The nitrogen nuclear spin and carbon-13 nuclear spins couple to the electronic spin through the hyperfine interaction (Fig. 3c), enabling selective manipulation of the electronic spin conditional on the state of the close-by nuclear spins^57,64. In addition, dynamical decoupling reduces the NV centre spin linewidths and allows for accessing and controlling more weakly-coupled nuclear spins^65,66,67. The NV centre thus serves as an ancillary qubit that provides access to the surrounding nuclear spin register. In this way the nuclear spins enlarge the qubit space and provide excellent memory qubits to the NV centre. Coherence times exceeding one second have already been observed for weakly coupled ¹³C spins at room temperature⁶⁸. In addition, nuclear spins cannot only be used as memory qubits but also as data processing qubits. Very recently two groups have implemented quantum error-correction protocols^69,70. By utilizing nearby nuclear spins they were able to demonstrate that the NV centre constitutes a fully functional quantum register that can serve as a node in a future quantum network.

An additional route towards enlarging the number of qubits per register is the fabrication of NV centre arrays. These arrays can be created through nitrogen ion implantation and subsequent annealing steps^71,72. Although the creation efficiency is still far from unity, ion implanting has already enabled a number of exciting experiments. One recent highlight is the observation of coherent magnetic coupling and quantum entanglement between two NV centres that were created at a distance of about 10 nm from each other⁷³.

Optical spin initialization, control and read-out. The NV electron spin can be initialized and read out using either off-resonant or resonant optical excitation. The first (off-resonant) method relies on a spin-dependent decay channel out of the excited state into a metastable singlet state. This causes the fluorescence to be spin-dependent, allowing for read-out. Furthermore, this process polarizes the electronic spin into the m_S = 0 ground state. However, the read-out contrast is small and therefore experiments have to be repeated many times. Furthermore, the initialization fidelities using off-resonant excitation seem to be limited to about 90% (refs 74,75). These issues can be overcome by using resonant optical excitation. At temperatures below 10 K the ZPL exhibits a spectrum made up from well-separated optical transitions (Fig. 4a). In high-quality crystals the linewidth of these transitions can be lifetime-limited. For low-strain NV centres these lines correspond to spin-selective optical transitions that enable the implementation of high-fidelity (>99.7%) initialization by optical pumping⁷⁴ (Fig. 4b, right). Furthermore, using a solid-immersion lens that enabled enhanced collection efficiencies of the emitted photons together with well-cycling spin-selective transitions, high-fidelity spin read-out has been achieved in a single-shot⁷⁴ (Fig. 4b, left). These initialization and read-out techniques can be extended to the nearby nuclear spins by mapping the state of the nucleus onto the electronic spin through selective microwave pulses and then reading out the electron⁶⁴. In this way, measurement-based initialization and single-shot read-out of small nuclear spin registers surrounding the NV centre have been demonstrated^{68,69,76,77,78}.

Figure 4: The optical interface of the NV centre.

a, The spectrum of the NV centre consists of a broad phonon sideband and a narrow ZPL at 637 nm. Within the ZPL several narrow resonances can be detected by scanning a laser across the resonance and detecting the red-shifted photons. Transitions are labelled according to the symmetry of their excited states. MW, microwave. Reproduced from ref. 74, NPG. b, For low-strain centres these transitions are spin-selective and can be used to initialize the spin state through spin pumping (right) and to read out the spin state in a single shot (left). Reproduced from ref. 74, NPG. c, It is possible to create entanglement between the spin and an emitted photon by using a lambda transition. The A₂ excited state decays simultaneously to the |m_S〉 = |+1〉 and |−1〉 ground state while emitting a photon whose polarization is entangled with the spin state. d, Indistinguishable photons emitted from two separate NV centres interfere on a beamsplitter and leave through the same output port. These photons are obtained by spectrally separating the ZPL emission from the phonon sideband emission. Reproduced from ref. 9, NPG. e, Schematic of the protocol to entangle two distant NV centres. The photons that are emitted from the two NV centres and that are entangled with their electronic spin are overlapped on a beamsplitter. Certain detection events in the output ports of the beamsplitter project the two spins onto an entangled state. Reproduced from ref. 12, MRS. f, The measurement results on the spin states in different bases (Z, Z and X, X) are strongly correlated and thereby prove the entanglement between the two distant spins.

For the above-mentioned techniques the optical interface of the NV centre is used incoherently, relying only on the spin-dependent properties of the optical transitions. However, at temperatures below 10 K the optical transitions can also be used coherently^79,80,81, which adds further control and sensing capabilities, and the possibility to link distant NV centres. Spin rotations along one axis can be induced through the AC Stark shift exerted by a spin-dependent, off-resonant light field⁸². The same effect can in principle be used to generate spin–light entanglement for linking remote spins registers. The NV centre also exhibits several Λ-type transitions (Fig. 4c). By applying two lasers, with different frequencies, to the NV centre, the system can be coherently trapped in a ground state superposition that is not excited⁷⁹. By varying the relative phase between the two light fields, it is possible to fully control the electronic spin by optical means^83,84. Additionally, these coherent population trapping techniques enable a sensitive probe of the nuclear spin environment through the shift that this environment causes on the transition frequencies⁸⁵.

Linking distant NV spin registers. The coherent optical interface of the NV centre opens the possibility to connect distant spins and construct a large-scale quantum network made from spin registers in diamond¹². In such a network individual nodes that are capable of generating, storing and processing quantum information are quantum mechanically connected to each other through a photonic channel. The first demonstration of a coherent photonic interface on the NV centre was the generation of entanglement between a single photon and the NV electron spin through the use of the Λ-type level structure shown in Fig. 4c (ref. 4). The A₂ orbital decays with equal probability into either the m_S = +1 or the m_S = −1 ground state, emitting a σ⁻ or σ⁺ polarized photon, respectively. This process can happen coherently, producing the spin–photon state (1/√2)(|+1, σ⁻〉 + |−1, σ⁺〉), which constitutes a Bell state.

Spin–photon entangled states can be used to create entanglement between two distant NV centres—a key primitive for a quantum network. In 2013 the generation of entanglement between two NV centres separated by three metres was achieved—the first entanglement between qubits on different solid-state chips⁹. This result was obtained in two steps. First, a spin–photon entangled pair was created at each NV centre. Then, the two photonic parts were measured jointly in the Bell basis by overlapping the photons on a beamsplitter and detecting photons in the output ports. A successful projection of the photons into a Bell state is signalled by a particular detection pattern in the output ports of the beamsplitter (Fig. 4d–f). Through the previously established spin–photon correlation, this detection simultaneously projects the two distant spins into an entangled state. This experiment was based on photonic time-bin qubits. These states are particularly suited for distributing entanglement over large distances, as they are robust against birefringence and polarization-dependent losses that occur in optical fibres. Sharing entanglement between two distant locations is a very valuable resource that can, for instance, be used to transfer a quantum state through quantum teleportation. This principle has very recently been realized with two distant NV centers¹⁰. In this experiment, the state of the nitrogen nuclear spin was teleported over a distance of three metres by consuming an entangled state that was shared between the electronic spins of the two NV centres. By using three matter qubits the quantum state could be teleported unconditionally (that is, each attempt to teleport succeeded). The teleportation fidelity reached 86%, clearly passing the classical threshold of 2/3. From this value the fidelity of the spin–spin entanglement can be estimated to be 87%. In this experiment the entanglement generation rate was 1/250 s⁻¹.

Towards a quantum network with NV centres. The entanglement between distant NV centres opens the way to extended quantum communication and measurement-based quantum computation experiments. Several challenges remain, which we briefly discuss. First, the probability of coherent photon emission (meaning photon emission without phonon excitation) is only around 3% due to coupling of the optical transitions to vibronic modes (Fig. 4a). Combined with the typically low detection efficiency of a confocal microscope set-up (a few per cent), this leads to a success probability of approximately 10⁻⁷ for creating an entangled state between two NV centres. To create a more efficient optical interface, a substantial effort has been geared towards establishing photonic cavities resonant with the ZPL. Both hybrid designs^86,87 and all-diamond approaches⁸⁸ have shown much promise, with Purcell factors of 70 reported⁸⁹. Note that a cavity will also dramatically enhance the collection efficiency from the NV centre. A second challenge is the high loss of photons in optical fibres at the ZPL wavelength (637 nm). One approach is to coherently convert the photons to telecom wavelength using nonlinear downconversion⁹⁰. Third, a quantum memory that is robust under optical excitation has to be incorporated. Nuclear spins that are close to the NV centre (within a few lattice spacings) dephase rapidly when the NV electron spin is optically excited^91,92. Instead, nuclear spins that are more weakly coupled have shown long coherence times (beyond a second) under optical excitation⁶⁸, and form a promising route towards realizing multi-node quantum networks in the coming years.

Alternative centres and rare-earth-ion doped crystals

The success of NV centres in the area of quantum optics and spintronics has spurred research into finding different defects with even better optical properties or within a different host material that could be more suitable for device fabrication. Within diamond, efforts have been focused mostly on centres that exhibit a strong ZPL, for use as single-photon sources⁹³. For instance, recently discovered colour centres that have been tied to chromium impurities have been used in on-chip quantum optical circuits⁹⁴. An exception is the SiV centre whose spin states have recently attracted (renewed) interest in the context of spin–photon interfaces⁹⁵. Very recently, two-photon interference between two SiV centres has been observed⁹⁶.

David Awschalom and co-workers have taken a different route. They started a quest to look for defects with properties similar to that of the NV centre but hosted in a more fabrication-friendly material. Theoretical considerations yielded a list of promising centres in a range of wide-bandgap materials⁹⁷. The first results were soon after reported on defect centres in silicon carbide (SiC) (ref. 98), a material that is used extensively in the optoelectronics industry (Fig. 5a–c). Room-temperature spin properties were found to be very similar to those of diamond spins^99,100. Under off-resonant optical excitation, the electron spin polarizes significantly. Also, the fluorescence is spin-dependent, allowing for room-temperature spin read-out. In many ways the current status with SiC is similar to that of NV centres a decade ago, and indeed current efforts have reached the single-spin limit^101,102 and focus on creating photonic nanostructures for efficient spin-photon interfacing¹⁰³.

Figure 5: Spins in silicon carbide and rare-earth-doped crystals.

a, Implanted n-type 4H-SiC spin ensembles. Different stackings of the crystal lead to different polytypes with their own individual spin characteristics as revealed by their optically detected magnetic resonance spectrum. b, These spin ensembles can be coherently manipulated by applying microwave pulses. I_PL represents the photoluminescence (PL) intensity. c, A Ramsey measurement shows a dephasing time of 250 ns. d, Electronic level structure of a Ce³⁺ ion in a YAG crystal. Using circularly polarized light, transitions between the lowest 4f and the lowest 5d spin doublets can be selectively addressed. e, Individual dopants can be detected in a confocal microscope set-up and show clear antibunching behaviour. f, The spin states can be manipulated coherently. Decoupling them from the environment leads to a coherence time, T₂, of 2 ms at 4 K. Panels a–c are reproduced from ref. 100, NPG. Panels d–f are reproduced from ref. 107, NPG.

Another interesting platform for quantum photonics is given by rare-earth ions doped in a crystal (Fig. 5d–f). The unique feature of these systems is the efficient screening of the inner electron shells from the surroundings. Whereas the outer shells interact and hybridize with the host lattice, the inner shell electronic properties are akin to those of isolated atoms. This behaviour promises long coherence times and robustness against electrical noise and thereby negligible spectral diffusion. Rare-earth impurities have been studied for decades and have become important in several photonic technologies, but single-impurity studies have until recently remained elusive. In the past two years, a number of ground-breaking experiments have reached the single-impurity limit. In one case, a single erbium ion implanted into silicon was investigated using a combination of spin-dependent ionization through resonant optical excitation and subsequent electrical on-chip charge sensing¹⁰⁴. Other experiments have detected a single praseodymium ion^105,106 and a single caesium ion by optical excitation and fluorescence detection¹⁰⁷. These studies may be the start of a new field in quantum spin photonics in which the efficient isolation of electronic levels within a solid-state host is harnessed for quantum information applications.

Challenges and outlooks

Photon extraction remains the principal challenge in realizing an efficient spin–photon interface using either NV centre or QD spins. Possible avenues for enhancing the photon collection efficiency include embedding the emitters in nanowires^108,109,110 or in photonic structures that realize the weak- or strong-coupling regime of cavity quantum electrodynamics (QED).

When the cavity–emitter coupling strength, g_C, is large compared with the spontaneous emission rate, Γ, but small compared with the cavity loss rate, κ, the coupled emitter–cavity system is in the weak-coupling regime, where the Purcell effect modifies the radiative decay rate of the emitter. Provided that the emitter is resonant with the cavity and its dipole is oriented along the cavity electric field at the emitter location, the decay rate is enhanced by a Purcell factor F_P = ((3λ³)/(4π²))Q/V_C, with V_C and Q denoting the cavity volume and the quality factor, respectively. F_P underlies the importance of confining photons in small structures with little loss. The increase of the decay rate will enhance the radiative efficiency and make the emission robust against dephasing, thereby enhancing the photon indistinguishability¹¹¹. Moreover, the Purcell effect can increase the photon extraction efficiency, as the fraction of photon emission into the cavity mode approximately scales as F_P/(F_P + 1) (ref. 112). Unlike the dipolar emission pattern of isolated emitters, the cavity output for many structures has a low-numerical-aperture Gaussian profile, allowing for efficient coupling to single-mode fibres. For NV centres, the Purcell effect plays an even more crucial role as the weight of the ZPL can be largely enhanced. Recent experiments have demonstrated 70% of the photons emitted in the ZPL⁸⁹.

The possibility of enhancing photon collection efficiency to a near-unity level using cavity-QED will enable an alternative, deterministic avenue for distant spin entanglement. In the strong-coupling regime, where g_C is larger than all relevant energy scales, it has been theoretically¹⁴ shown that it is possible to reliably convert quantum information from a spin-qubit to a flying photonic qubit or vice versa¹¹³. Starting out with an entangled spin–photon pair, we can then faithfully transfer the quantum information into a second distant spin qubit using cavity-QED, thereby creating (near) deterministic entanglement of distant spins (Fig. 6a). We also note that it is possible to induce a spin-state-dependent giant Kerr or Faraday rotation of the incident photons with the help of cavities. Recently, large Kerr rotations for a single spin coupled to a cavity have been experimentally demonstrated¹¹⁴. Theoretical work has shown that it is possible to use such an off-resonant interaction to implement a deterministic spin–photon gate or entanglement^115,116,117 (Fig. 6b), which has been demonstrated in atomic systems¹¹⁸. Even so, in the unavoidable presence of photon loss such schemes will likely need to be supplemented with photon-arrival detection to herald the success of the protocol.

Figure 6: Spin photonics networks.

a, Entanglement of distant spins through photonic quantum information transfer. Two nearby spins are assumed to be entangled. After the first spin qubit is converted into a flying photonic qubit, the second spin becomes entangled with the propagating photon. When the photonic information is transferred to a third spin in another cavity, the spins in the two distant cavities (nodes) are entangled. This process can be near-deterministic. b, Linking of distant nodes by a spin–photon gate. A spin-tagged QD optical transition that couples strongly to a cavity mode induces a giant Kerr or Faraday rotation of the incident coherent field, which can be used to link different nodes in a network. c, On-chip spin–spin entanglement generation by projective photonic measurement. Two pairs of spin–photon entangled states are generated separately. The photons are sent to a waveguide beamsplitter for two-photon interference. When a photon coincidence is detected by on-chip superconducting detectors, entangled spin-pairs are generated. d, Linking of distant nodes by projective photonic measurement. Each node consists of several entangled spin-pairs, one of the spin qubits is converted to a photonic qubit, which is subsequently sent to a two-photon interferometer. Upon coincidence detection in a Hong–Ou–Mandel interferometer, distant nodes share an entangled spin pair.

To achieve scalability, active engineering efforts are required such as on-chip integration of emitters, photonic circuits and detectors. It has already been demonstrated that QDs can be coupled to photonic nanostructures¹¹⁹ incorporating photonic crystal cavities^{30,120,121,122}, waveguides¹²³ and nanowire superconducting detectors¹²⁴ (Fig. 6c). These advances suggest that the generation, routing and detection of photons can all be integrated onto the same chip¹²⁵. An all-integrated platform will be of particular interest for realizing local quantum networks based on interconnected small-scale quantum information processors (Fig. 6b,d).